Exploring Strongly Connected Components and the Kosaraju Algorithm

Understanding Strongly Connected Components and the Kosaraju Algorithm for Graph Analysis

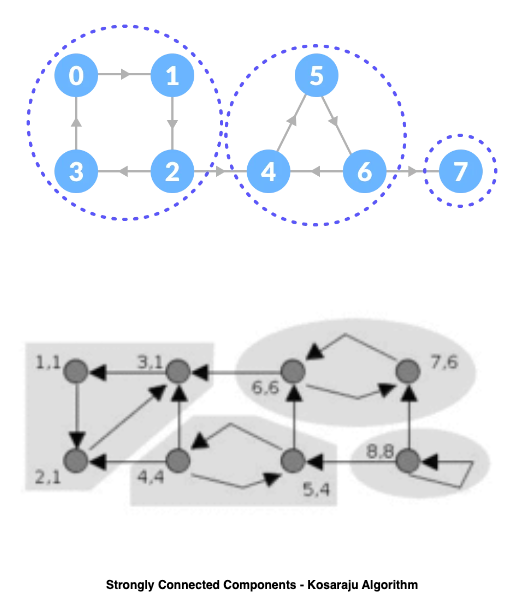
In the field of graph theory, understanding the connectivity and structure of networks is of paramount importance. Strongly Connected Components (SCCs) play a significant role in analyzing the relationships and dependencies within a graph.

In this blog post, we will delve into the concept of SCCs and explore the Kosaraju Algorithm, a widely used method for identifying SCCs in a graph.

1. Understanding Strongly Connected Components: Strongly Connected Components are subsets of vertices within a directed graph where every vertex is reachable from every other vertex in the subset. In simpler terms, it represents a group of nodes that can reach each other through directed paths. SCCs provide insights into the cohesive substructures and interconnections within a graph.
2. Kosaraju Algorithm: The Kosaraju Algorithm is an efficient algorithm for finding SCCs in a directed graph. It consists of two passes over the graph, known as the “forward” and “backward” passes. Let’s explore the steps involved in the Kosaraju Algorithm:

• Step 1: Perform a Depth-First Search (DFS) in the forward pass: Start a DFS from each unvisited vertex, traversing the graph in a depth-first manner. Maintain a stack to keep track of the order in which vertices are visited.
• Step 2: Reverse the graph: Reverse the direction of all edges in the graph, creating a new graph.
• Step 3: Perform a Depth-First Search (DFS) in the backward pass: Pop vertices from the stack obtained in the forward pass and start a DFS from each unvisited vertex in the reversed graph. The SCCs are identified during this pass.
• Step 4: Output the SCCs: Each completed DFS traversal in the backward pass represents an SCC. Collect the vertices visited in each traversal and output them as separate SCCs.

PySpark Implementation of the Kosaraju Algorithm: PySpark provides a convenient and scalable framework for implementing graph algorithms like the Kosaraju Algorithm. Below is a code snippet demonstrating the PySpark implementation:

from pyspark.sql import SparkSession 
from graphframes import GraphFrame  

spark = SparkSession.builder.getOrCreate()  

# Create a graph frame from vertices and edges data 
vertices = spark.createDataFrame([(1,), (2,), (3,), (4,), (5,)], ["id"]) 
edges = spark.createDataFrame([(1, 2), (2, 3), (3, 1), (4, 5)], ["src", "dst"])

graph = GraphFrame(vertices, edges)  

# Apply the Kosaraju Algorithm to find SCCs 
scc = graph.stronglyConnectedComponents()  

# Display the SCCs 
scc.show()

Applications of Strongly Connected Components:

• Web Analysis: SCCs help identify communities or clusters of related web pages or websites.
• Social Network Analysis: SCCs reveal closely connected groups of individuals or communities within social networks.
• Compiler Optimization: SCCs aid in optimizing code generation by identifying independent code blocks.

Understanding Strongly Connected Components and the Kosaraju Algorithm allows us to gain insights into the structure and connectivity of complex graphs. By leveraging PySpark’s capabilities, we can efficiently analyze large-scale graphs and extract valuable information from them. SCCs have various applications in diverse domains, from web analysis to social network analysis and compiler optimization. Start exploring SCCs and unleash their power in analyzing graph data!

By following the steps of the Kosaraju Algorithm and utilizing PySpark’s graph processing capabilities, you can efficiently identify Strongly Connected Components in your graph data and gain deeper insights into its underlying structure and connectivity.